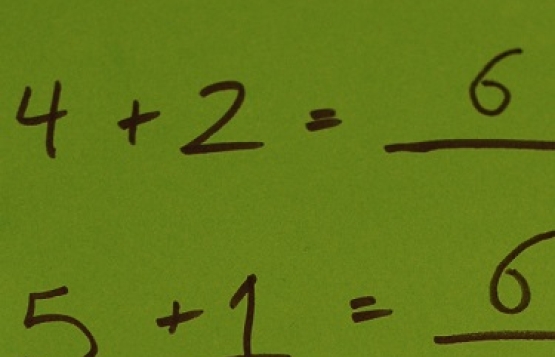
Responding to critics of Common Core math in the elementary grades
Their criticisms don’t add up. Robert Pondicio and Kevin Mahnken
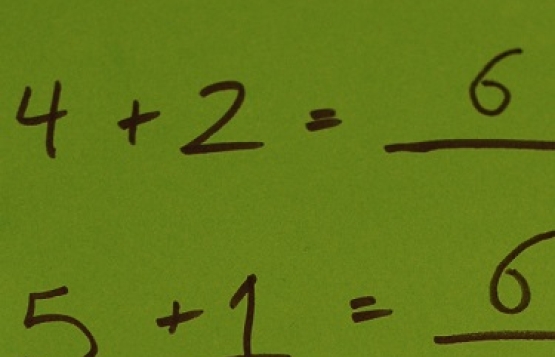
Their criticisms don’t add up. Robert Pondicio and Kevin Mahnken







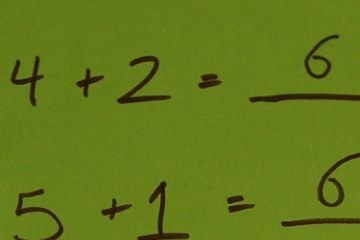

Common Core has the potential to shift and drastically improve math instruction in American schools, but its detractors have marshalled a raucous opposition to its proposed changes. We’ve already examined the questionable arguments against Common Core literacy standards; now we’re turning our sights to math.
September’s Intelligence Squared U.S. debate pitted Fordham President Michael J. Petrilli and the Center for American Progress’s Carmel Martin against the American Enterprise Institute’s Rick Hess and New York principal Carol Burris. Hess and Burris are two of Common Core’s most eloquent and energetic critics, but the position they mounted against the initiative’s math standards is not a strong one. It can essentially be boiled down to three points:
1.) The standards confuse children.
This is perhaps the most common critique of Common Core math. As the new standards have been implemented (seldom perfectly) in participating states, districts, and schools, children have sometimes been assigned math problems that would make a structural engineer scratch her head. Parents accustomed to the “classic style” of teaching math—long worksheets of standard algorithms with one or two word problems at the bottom—worry about the unfamiliar presentation of their kids’ homework, and many opponents have delighted in picking apart often inscrutable questions. At the debate, Burris recited a confusing-sounding Common Core standard (1.OA.C.6) for teaching young students:
Here’s a first grade example. “Use strategies such as counting on; making ten (e.g., 8+6 = 8+2+4 = 10+4 = 14); decomposing a number leading to a ten (e.g., 13-4 = 13-3-1 = 9)…and creating equivalent but easier or known sums (e.g., adding 6+7 by creating the known equivalent 6+6+1 = 12+1 = 13).” Now, when you listen to that, are we surprised that we have created complicated homework problems that comedians joke about and that make children cry?
We’d cry too if a first-grade teacher read that standard to a six-year-old. Tellingly (and almost for certain deliberately), Burris leaves out the first sentence of the standard: “Add and subtract within 20, demonstrating fluency for addition and subtraction within 10.” That’s plenty clear. But crucially, standards aren’t written for children, they’re written for professionals—those highly trained and trustworthy teachers that Burris rightly lionizes as experts—not for students. A recent short video by Robert Hanna of the Center for American Progress makes precisely the same point—there’s a difference between what a standard says and what that would look like in a classroom. A teacher would no sooner read this kind of guidance to a seven-year-old than a waiter would recite food-handling procedures to a diner who merely wants to know what’s on the menu tonight.
The standard in question asks teachers to ensure that students understand and can work fluently with numbers within 20. The methods listed here are commonplace in countries like Singapore and Japan. First-graders should be able to see, for example, that 8+7 gives you the same sum as 10+5. Or that 13-4 equals 13-3-1. If you know that 8+4 = 12, you also know that 12-4 = 8. This is neither inscrutable nor too much to ask of a first-grader. Surely we want them to be able to “add and subtract within 20.” Note too the use of the phrase “such as.” There are myriad ways for teachers to interpret these standards for students to ensure fluency; these are but a few examples.
To be sure—and to be fair—there is much room for concern about the uneven quality of curriculum and instruction, a problem that Common Core has done less to create than to reveal. And the incipient stages of Common Core implementation haven’t always proceeded smoothly. But conflating guidance for teachers with the work that’s put in front of children is a lazy tactic meant to obscure the truth: Common Core’s “new” approach to math isn’t new, it’s actually very understandable, and kids have already proven adept at grasping it—despite the higher level of rigor the standards demand of students, teachers, and parents.
2.) Young students just can’t handle it.
Burris often wields the phrase “developmentally inappropriate” as a cudgel against Common Core. It’s a weighty-sounding bit of education-ese that carries the authority of science. The implication is that Common Core is demanding a type of thinking that children are simply not capable of. But as Dan Willingham has pointed out, the “stage theory” approach to learning has two major problems: “First, data from the last twenty years or so make development look like it's continuous, rather than occurring in discrete stages. Second, children's cognition is fairly variable day to day, even when the same child tries the same task.” According to Willingham, developmental psychology is not a useful guide to determining what children should learn and when.
…[Y]ou can't always wait until children are “ready.” Think about mathematics. Children are born understanding numerosity, but they understand it on a logarithmic scale—the difference between five and ten is larger than the difference between 70 and 75. To understand elementary mathematics they must learn to think of numbers of a linear scale. In this case, teachers have to undo Nature. And if you wait until the child is “developmentally ready” to understand numbers this way, you'll never teach them mathematics. It will never happen.
In short, Burris is wrong to claim that certain material can simply be disqualified from curricula on the basis of age. One of the lead writers of the Common Core math standards, Jason Zimba, adds that Burris’s knowledge of standards is also outdated:
While it is true that many of the oldest state standards only asked kindergarten students to count to 20, more recent standards went higher, to “at least 20” or “at least 31” or up to 100 (see Washington D.C., Georgia, Minnesota, Virginia, and Washington). One reason older standards were limited to 20 was that those standards didn’t distinguish clearly between rote-counting (saying the number words) and cardinal-counting (telling how many). CCSS makes this crucial distinction evident. The National Research Council’s report “Mathematics Learning in Early Childhood: Paths Toward Excellence and Equity” is also clear that counting to 100 is appropriate in kindergarten.
Burris also skips over another critical distinction—proponents of the standards don’t demand that students grasp all the components of rigor (fluency, conceptual understanding, and application) when working with numbers between 20 and 100, rather that they familiarize themselves with the larger quantities as a basis for future learning. Learning both simpler and less intuitive math concepts simultaneously strengthens a student’s understanding of both. Zimba points to a recent longitudinal study by the University of Missouri’s David C. Geary, who notes that the kind of math that kindergarten students learn under Common Core—and which Burris calls developmentally inappropriate—is predictive of math literacy many years later.
California kindergarten teacher Robbie Torney, in a response to Burris published on Real Clear Education, wrote that “[n]ot only should kindergarteners be able to count to 100—as noted in the Common Core—but they can. How to get them there is part of the art and science of teaching and involves making sure that I know what my students know and can move them to where they need to be.” Burris has no convincing answer to this.
The bottom line is that “developmentally inappropriate” is too often used as a shut-down phrase, one that adds little to debate or understanding. If we know where we want kids to be at the end of 13 years of schooling, delaying learning is the intellectual equivalent of a balloon payment on a mortgage. Sooner or later, it’s got to be paid up.
3.) Too much emphasis on abstract mathematical concepts.
Combatants in the math wars tend—like people in the old Miller Lite commercials yelling “tastes great!” and “less filling!” at each other—to fetishize either procedural fluency or inquiry-based teaching techniques. They lampoon the other side as favoring “drill and kill” or wanting students to invent their own algorithms, stumbling blindly forward in hopes of intuiting their way to the Pythagorean theorem. But clearly, kids need both the ability to compute with speed and accuracy, to understand the answer they got, and to know and whether it makes sense.
Common Core certainly does challenge students to comprehend math at the conceptual level—the broad strokes of composing and decomposing numbers, for instance—but only in concert with, and not opposed to, mastering standard algorithms. If there are math-education leaders out there denigrating exact computation in the name of the Common Core, then the best way to correct them is to point out these expectations in the standards themselves.
The standards call for teachers to pursue, as appropriate, three components of rigor in math education: Conceptual understanding, fluency, and application. Nowhere is it claimed that one component is most important.
Stressing conceptual understanding of math is by no means a new approach to teaching the subject. It’s a well-known, well-respected technique that veteran teachers have favored for years. Higher-order math principles can easily be taught alongside the popular tricks and shortcuts that help younger children find the answers to tough problems; but Common Core doesn’t mandate that math be taught that way because (repeat after me) Common Core is not a curriculum.
Events like the Intelligence Squared U.S. forum are useful vehicles for the exchange of ideas and reasoned argument. Burris and Hess are credible spokesmen for their point of view, and it should be obvious by now that neither side of this debate is immune from criticism. But when your case against Common Core leans so heavily on muddled logic and flawed science, it suggests that your arguments don’t add up.
photo credit: Mandajuice via photopin cc


“Ambiguous” is a reliably fun word to teach sixth graders. They quickly grasp its essence and utility. I introduce it by explaining how I was once given a keychain with the legend “I Teach. I Make a Difference.” I assure my students that I have never used this keychain, for, in keeping with my unyielding commitment to personal excellence, I would only ever boast of making a positive difference. Then we have a lively discussion about the possible meanings of the keychain’s phrase. This discourse was evidently not forgotten by one student, who in June concluded a speech, "Mr. Sipe, you made a difference." Then she smiled wickedly and added, “A big difference!”
At least she didn’t declare this: “He could not disguise from my hourly notice the poverty and meagreness of his understanding.” That unambiguous teacher evaluation was penned by Thomas DeQuincey almost two hundred years ago in Confessions of an Opium-Eater. He dispatches another master as “a blockhead, who was in a perpetual panic lest I should expose his ignorance.” You don’t have to read far to begin to wonder if his titular waywardness was perhaps due to unrewarding schooling. “It is a bad thing,” DeQuincey observes, “for a boy to be and to know himself far beyond his tutors, whether in knowledge or in power of mind.” I wouldn’t challenge him on this.
The question of how to challenge a young Thomas DeQuincey is not merely academic—it’s entirely academic: I teach reading to about a hundred students a year, each of whom must spend a daily hour with me. I don't think it's unreasonable to expect at least one young Thomas per crop. Uncle Sam can speak loudly and carry a big stick when it comes to altering my instruction for students classified with learning disabilities, but he minds less how I teach those with learning gifts. While I can cut some rug in the differentiation dance, I just don’t see how I could slice my curriculum or my instruction to young Thomas’s satisfaction.
Students can be as quiet about their gifts as Uncle Sam is, but young Thomas was not. A beloved teacher said of him, “That boy could harangue an Athenian mob better than you or I could address an English one.” Given DeQuincey’s schoolboy hobby of translating newspapers into Greek, I suspect his contempt for our unit on The Adventures of Ulysses would be Homeric.
DeQuincey was not the only English writer dissatisfied by school. W. Somerset Maugham, humiliated for his speech impediment, wrote that his school “looked upon learning with suspicion.” In “Such, Such Were the Joys,” George Orwell shares his enduring understanding: “Failure behind me, failure ahead of me—that was by far the deepest conviction that I carried away.” Roald Dahl’s portraits of cruel and stupid masters in Boy are indelible. And about the least damning thing Morrissey has to say about school in last year’s Autobiography is this: “Exactly why I am here, and what it is I am meant to do, is beyond me.”
While it could be argued that their schooling may have contributed to later achievements—you don't, at least, get the sense that these authors struggled with writer’s block on the subject of school—it certainly didn’t nurture their gifts. On the other hand, there's no denying that their teachers challenged them. You might even say their teachers made a big difference.
Which brings me back to the question of how I can make a difference for my gifted students. What these authors wrote about school does offer guidance. I find it instructive that they seem to have gained their erudition despite school, not because of it. Accordingly, I don't think young DeQuincey et al. would much need a sixth-grade reading teacher.
But perhaps they could use a helpful librarian. I'd recommend that DeQuincey read Somerset Maugham's The Lotus Eater as a cautionary tale, and I'd lend Maugham Black Swan Green by David Mitchell, so he'd know he's not the only stammerer having a rough time at school. Mitchell, it’s worth pointing out, recalls “three or four gifted teachers.…They exposed me to some fine writers and encouraged my covert bookishness.” I don’t, thank heaven, have to be gifted to do that. Nor would I even have to be talented to afford George Orwell one of his few respites from scholastic misery, “getting in an hour's undisturbed reading."
I first read Orwell’s “Such, Such Were the Joys” long before I became a teacher. Then I read it with satisfaction, understanding it as justifiable retribution. Now it's tough to read, especially sentences like this:
This business of being out for a walk, coming across something of fascinating interest, and then being dragged away from it by a yell from the master, like a dog jerked onwards by the leash, is an important feature of school life, and helps to build up the conviction, so strong in many children, that the things you most want to do are always unattainable.
It's not, for various reasons, something that seems wise to explore at length in print, but I will say that fourteen years of teaching and fifteen months of fatherhood have brought to my repeated notice the useful preparation that dog ownership offers for both endeavors. Orwell's simile almost put a lump in my throat. It recalled the first time I took my grouchy terrier, Roosevelt, to the seashore when he was a puppy. What happened next was the revelation that unbridled joy is not always a figure of speech. To very gingerly pursue this metaphor, I wouldn't take the collar off young Eric Blair during our daily hour; but I'd like to think that the most I'd pull his leash would be to propose that, although "George" was a fine start, perhaps he could come up with a better surname.
“When your gift unfurls," Morrissey sings on a B-side. Morrissey singles are my kind of professional development, and his (more politic) metaphor indicates how this reading teacher can make a difference: I can help undo a knot here or there and lend a hand to move those gifts from a flutter to a flap. The biggest, most positive difference I can make for gifted students is to differentiate between my instruction and my interference.
I’m sure I’d disguise nothing from young Thomas’s hourly notice, nor would I be likely to escape his pen. But neither would I want him to record our hours as wasted. For, as he concludes, though not without a note of ambiguity, "At that happy age, if no definite boundary can be assigned to one's power, the spirit of hope and pleasure makes it virtually infinite.”
Peter Sipe teaches at Boston Collegiate Charter School. For more by Peter, read his July post for Flypaper.
photo credit: CollegeDegrees360 via photopin cc



Mayor de Blasio’s school plan, low American math scores, the intersection of standards and charters, and school management.
Amber's Research Minute
Nicholas Bloom, Renata Lemos, Raffaella Sadun, and John Van Reenen, "Does Management Matter in Schools," National Bureau of Economic Research, Working Paper 20667 (November 2014).

Sometimes the conventional wisdom is right. Education really is an easy major. This study from the National Council on Teacher Quality, the bête noire of America’s teacher prep programs, finds that 44 percent of prospective teachers graduate with honors, compared to only 30 percent of all graduating students at the same colleges. The reason appears to be that grading standards for education majors are much lower than for students in other majors on the same campus. NCTQ analyzed course assignments on the syllabi for nearly 1200 courses at thirty-three schools—not just in education, but in a variety of majors. The 7,500 assignments in those courses were then classified as either “criterion-referenced” or “criterion-deficient.” The former means that students were graded on “a clearly circumscribed slice of knowledge and skill-based content,” which ostensibly allows instructors to provide substantive feedback and comparisons of student work. By contrast, “criterion-deficient” assignments were more subjective in nature. These latter kinds of assignments are used about twice as often—71 percent versus 34 percent—in education coursework. The report also examines and dismisses several popular theories for why ed majors earn so many As: Yes, a rising tide of grade inflation has lifted all boats, but teacher candidates’ boats are like hovercraft rising above the waves. Interestingly, the assumption that ed school is all low-level assignments and group work turns out to be a canard—as is the less commonly held belief that ed students and faculty are simply stronger than other departments. “If one believes in training teachers by equipping them with effective techniques, then having criterion-referenced assignments is essential,” the report concludes. Mighty big “if.” The schools covered in NCTQ’s report train—well, credential—half of the country’s annual crop of new teachers. If they enter the classroom without having practiced and mastered the content and skills they need to be effective, they begin their careers already behind.
SOURCE: Hannah Putman, Julie Greenberg, and Kate Walsh, “Training our future teachers: Easy A’s and what’s behind them,” National Council on Teacher Quality (November 2014).

This new study examines whether voluntary financial contributions to public education have increased over time and, if so, whether these donations vary by district size and other characteristics. Voluntary contributions are those awarded by charitable school foundations, local endowments, booster clubs, parent-teacher associations, and alumni associations—so these are local dollars in addition to the local revenues generated largely by property taxes. Analysts examine voluntary contributions to public schools from 1995 through 2010, relying on Form 990 filings that are captured in the Guidestar nonprofit database, which includes expenditure reports for nonprofits with annual revenues totaling $25,000 or more. These data were then linked with mapping data to match the nonprofit to the corresponding school district, including data about district revenues and demographics. The final sample included over 13,000 non-profits that supported schools and/or districts. There are four key findings. First, PTAs comprise most of the nonprofits (70 percent), while local foundations comprise only 13 percent. And among all donors, 93 percent of them give to district schools, while only 1.3 percent support charter schools. Second, the number of nonprofits supporting schools has increased 230 percent, from over 3,400 in 1995 to nearly 12,000 in 2010. Third, nonprofit revenues increased almost 350 percent, from $197 million in 1995 to $880 million in 2010. Nationwide, per-pupil voluntary contributions jumped along with it, going from $3.67 in 1995 to $20.31 in 2010. Moreover, if you hone in on those districts that have at least one non-profit supporting them, we see that the voluntary giving grew from $8.02 per pupil in 1995 to $28.38 in 2010. Still, these contributions are a drop in the bucket when you recognize that public schools spent an average of $10,615 per student in 2010. That said, the fourth and final key point is that certain larger districts have a higher likelihood of receiving nonprofit contributions—those with higher property tax revenues per pupil; more educated and wealthy residents; lower unemployment; and lower proportions of kids who are non-US citizens, are living in poverty, or reside in female-headed households. In other words, nonprofits enhance spending in districts that already receive significantly larger per-pupil revenues, which isn’t terribly surprising. After all, the wealth is greater in these districts. And who wants to tell PTAs that they can’t raise extra money for their kids’ schools?
SOURCE: Ashlyn Aiko Nelson and Beth Gazley, "The Rise of School-Supporting Nonprofits," Association for Education Finance and Policy (Feburary 2014).

This book, out of the Clayton Christensen Institute for Disruptive Innovation, is a useful field guide to the design and implementation of blended learning models, which combine computer-mediated resources like MOOCs with conventional classroom instruction. Nonetheless, readers may greet its subtitle, “Using Disruptive Innovation to Improve Schools,” with a pang of foreboding. Blended initially makes you worry that its pages will mostly be a blend of TED Talk doublespeak. Indeed, the foreword (contributed by the High Prophet of Disruption himself, Clayton M. Christensen) ominously name-checks Thomas Kuhn, the philosopher and historian who first coined the now-inescapable phrase “paradigm shift.” But whatever their slight fondness for techno-jargon, authors Michael B. Horn and Heather Staker have written something valuable mainly because they are at pains to define their terms. This is the critical task facing advocates of blended learning, as Fordham itself has chronicled. Furnishing students with laptops and posting lesson plans on Blackboard isn’t blended learning; nor is a totally online experience that students access from home. For clarification, Horn and Staker use refreshingly simple graphics to outline the varying blends—from hybrid approaches shuttling kids between online activities, small-group instruction, and pen-and-paper assignments, to more unfamiliar models that explicitly make online teaching the backbone of coursework even within brick-and-mortar schools. The book doesn’t sidestep the question of what role teachers and facilities will play as more curriculum and tutoring is done remotely; the treatment is thin, but its vision of community schools providing family services, serving nutritious (and even edible) meals, and guiding socialization between students is an intriguing one. The concluding recommendations of reaching out to community stakeholders and phasing changes in slowly are ultimately commonsensical, but Blended has by this point already provided a detailed—and comprehensible—overview of how to introduce technology into the classroom without throwing tradition over the side.
SOURCE: Michael B. Horn and Heather Staker, Blended: Using Disruptive Innovation to Improve Schools, Jossey-Bass (November 2014)