The Education Gadfly Weekly

As a chubby girl at Treakle Elementary School (Mom said it was just “baby fat”), one thing I remember having to do was memorize my times tables. My well-meaning Dad and I sat at our kitchen table after dinner as he called out multiplication problems to me at lightning speed: six times six, twelve times eleven, eight times nine, ten times three. On and on it went. When I got one wrong (aargh!), he went back to it again (and again). Unnerving, to be sure, but I felt great pride at (eventually) memorizing the entire lot and I relished the ritual that Dad and I shared as Mom finished the dishes and my near-teen sister chatted forever on the phone.

I’ve since learned that not all teachers, kids, and parents are as smitten with memorizing fundamental math facts. Yes, some are adamant that kids must memorize the basics or they’ll fall ever farther behind. But others are just as convinced that memorization in elementary school damages youngsters academically and emotionally, stunting their genuine understanding of math concepts and leaving them frustrated, stressed, and math-averse.

Part of the rationale for academic standards is to standardize essential elements of what is taught and learned in core subjects of the K–12 curriculum. How that gets done is mostly left to the discretion of districts, schools, and teachers, but the fundamentals are supposed to be the same no matter where a student attends school.

Which brings us to the Common Core State Standards for math (CCSS-M). How do they treat the memorization of math facts?

Interestingly, the standards don’t ever use the word memorize. (Nor do they use the word automaticity.) Rather, they specify that students will know from memory their addition and multiplication facts by the end of grades two and three, respectively. One might assume that “know from memory” is synonymous with “memorize,” but apparently not. Some math folks say that there’s a big difference.

Yet I’m not alone in my confusion. In our latest report, Common Core Math in the K–8 Classroom, for instance, one grade-five teacher said, “Common Core is not the answer. Students do not know the basics needed to function in their grade level. Multiplication tables need to be memorized.” She seems to think that CCSS-M does not support memorization of multiplication facts (and who knows what she thinks of “knowing from memory”?).

To get to the bottom of how CCSS-M views memorization of math facts, I asked one of the lead writers of the Common Core Math standards: Jason Zimba. The questions below reflect our conversation.

Amber Northern: Is there a reason why the CCSS-M specify that students “know from memory” their addition and multiplication facts—versus simply “memorizing” them?

Jason Zimba: The standards require students to know basic facts. Here is the language for multiplication (page 23):

"By the end of Grade 3, know from memory all products of two one-digit numbers."

We can debate the best ways to help students meet this expectation, and we can debate the best ways to assess whether students have met the expectation. Those are good discussions to have. But there is no room to debate the expectation itself. The language in the standards is unambiguous.

I don't think the important issue here is the word choice involved in "memorize" versus "know from memory." That difference is technical: Memorizing most naturally refers to a process (such as the one you and your dad engaged in), whereas knowing more clearly refers to an end; and ends, not processes, are the appropriate subjects for a standards statement. When the teacher in your survey says, "Multiplication tables need to be memorized," I take the teacher to be saying that students need to know the multiplication table from memory. And I agree. Some experts don't, but as we can see from the text of the standards, their view did not prevail. I don't think anybody could find the sentence on page 23 unclear. I do know there are people who wish that the sentence had not been included. Perhaps their discomfort interferes with their reading comprehension.

AN: Some folks seem to think that “know from memory” also means “being fluent in.” Can you clarify the difference?

JZ: They aren't the same thing, and the language of the standards makes this clear. Let's look again at the standard on page 23, which reads in full as follows:

3.OA.C.7. Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 ´ 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.

The first sentence sets an expectation of fluency. The second sentence sets an expectation of knowing from memory. If being fluent were the same thing as knowing from memory, the second sentence would not have been necessary. That the second sentence was included shows that the two things are not the same.

In the context of arithmetic, the word "fluently" is used nine times in the standards; there is also one instance of the phrase "demonstrating fluency." In every case, fluency pertains to an act of calculation. In particular, to be fluent with these calculations is to be accurate and reasonably fast. However, memory is also fast, so the difference between fluency and memory isn't a matter of speed. The difference, rather, has to do with the different nature of calculating versus remembering. In an act of calculation, there is some logical sequence of steps. Retrieving a fact from memory, on the other hand, doesn't involve logic or steps. It's just remembering; it's just knowing. The mental actions of calculating and remembering are different. The standards expect students to remember basic facts and to be fluent in calculation. Neither is a substitute for the other.

Researchers in cognitive science could probably find fault with my description of the differences between calculating versus remembering as mental actions. Setting all that aside, it still remains the case that the standards as written plainly treat fluency and memory as two different things. According to the text of 3.OA.C.7, you haven't met the standard unless you know the products from memory—even if you are fluent in calculating products and quotients.

You said that some people seem to think that "know from memory" also means "being fluent in." I suspect that talking this way is something people do when they wish that the standards hadn't set an expectation of knowing from memory. Rhetorically, they try to write the word “memory” out of the standards. Of course, some people out there are actually writing the word out of the standards. Look at what happened to "knowing from memory" when Indiana and South Carolina revised the Common Core:

These two revision committees certainly weren't confused about the difference between fluency and memory. They kept the fluency part and got rid of the memory part. Maybe the teacher in your survey who complained about the times tables was from South Carolina? At any rate, if she's referring to the Common Core, then she's laboring under a misconception.

AN: And there are multiple ways to help students meet the standards’ expectation of knowing the facts from memory, yes?

JZ: Yes, people do use a variety of curriculum materials, whether those be flashcards, games, digital apps, or what have you.

AN: That brings me to a clarifying question on strategies. A few standards relative to operations and algebraic thinking (such as 1.OA, 2.O.A and 3.OA) refer to “mental strategies” such as “making ten” and “decomposing a number leading to a ten.” Is memorization also a “mental strategy” to know your math facts from memory? It is tautological in my mind!

JZ: No. The term “mental strategies” here means mathematical methods. I'm happy to shed light on this as long as it's clear from the start that knowing the addition facts from memory is expected (page 19). But in the course of things, students will be working with sums before they know all of them from memory. So mental strategies are what a student uses to calculate the answer during that period of time before she knows the answer from memory. For example, suppose the question is "8 + 7 = ?" A typical first grader, certainly early in the year, will calculate that answer rather than retrieving it from memory. She might think along these lines: One more than 7 + 7, which I remember is 14, so 15. Eventually—if the standards are being met—she doesn't need the calculation process because she just knows that the answer is 15.

Nor is "remembering" a mental strategy, since memory is handled separately from calculation altogether, in the second sentence of 2.OA.2.

Add and subtract within 20: Fluently add and subtract within 20 using mental strategies. By the end of Grade 2 know from memory all sums of two one-digit numbers.

AN: Let’s keep on the topic of strategies for another minute. You use flash cards with your kids to help them learn their math facts. Other teachers use games. Yet these are different from the “strategies” (like “make ten”) listed in the standards. Is it more accurate to call flash cards and such manipulatives? I know it seems minor, but I think we need to be clear about what a “strategy” means in the context of the standards and what it doesn’t mean—and where questions of pedagogy justifiably come into play.

JZ: When the standards refer to a strategy, it means a mathematical method, not a material object like flash cards or dice. I would classify flash cards as curriculum materials.

AN: Another topic that could use clarification is what the Progressions mean by “just know.” For those who aren’t aware, the Progressions are CCSS-M related documents that are not part of the standards, per se; however, thirteen of the fifteen Progressions writers also served on the standards development team. The documents show how a math topic gets developed across grade levels. The document, in explaining fluency, says that it partially involves “just knowing” some answers.[1] Here’s the reference:

The word fluent is used in the Standards to mean “fast and accurate.” Fluency in each grade involves a mixture of just knowing some answers, knowing some answers from patterns (e.g., “adding 0 yields the same number”), and knowing some answers from the use of strategies. It is important to push sensitively and encouragingly toward fluency of the designated numbers at each grade level, recognizing that fluency will be a mixture of these kinds of thinking which may differ across students…[A]s should be clear from the foregoing, this is not a matter of instilling facts divorced from their meanings, but rather as an outcome of a multi-year process that heavily involves the interplay of practice and reasoning.

How, if at all, is “just knowing” different from “knowing from memory”?

JZ: They mean the same thing. "Just knowing" is closer to the way a student would talk. ("How did you get the answer?" "I just knew!")  

AN: Is “instilling facts divorced from meaning” a critique of memorization?

JZ: Not unless you think that memorizing demands that we work in inefficient ways. Imagine you're a teacher working on the times tables with your students. Bear in mind, there are one hundred different single-digit products to learn. Here are nine of them: 1 ´ 1, 1 ´ 2, 1 ´ 3, 1 ´ 4, 1 ´ 5, 1 ´ 6, 1 ´ 7, 1 ´ 8, and 1 ´ 9. Will you really try to teach this batch as separate facts, divorced from their meanings? That would be colossally inefficient. Memorizing single-digit sums and products isn't like memorizing the alphabet. The alphabet is an irrational sequence with no structure or internal logic. It can't be optimal to memorize the addition and multiplication tables, with all their patterns, the same way we memorize the alphabet sequence. By pointing that out, I'm not critiquing memorization—I'm prompting us to think about the most effective way to reach the endpoint: knowing the single-digit sums and products from memory.

AN: Is it possible for children to memorize their addition and multiplication facts and understand what addition and multiplication mean?

JZ: Of course. Above, you linked to an article by an educator who is "adamant that students must memorize the basics." I clicked through, and that author also agrees: "Children need to understand the times tables, and they also need to memorize them."

AN: Thanks so much for your help, Jason, in clarifying this important issue. Any final thoughts?

JZ: Thank you, Amber. I thought there was some good advice for parents in the first article you linked to ("Why Learning the Times Tables is Really Important"). To that, I might add my own contribution from earlier this year on the Flypaper blog.

Ohio has finally proven that it is serious about cleaning up its charter sector, with Governor Kasich and the Ohio General Assembly placing sponsors (a.k.a. authorizers) at the center of a massive charter law overhaul. House Bill 2 aimed to hold Ohio’s sixty-plus authorizers more accountable—a strategy based on incentives to spur behavioral change among the gatekeepers of charter school quality. Poorly performing sponsors would be penalized, putting a stop to the fly-by-night, ill-vetted schools that gave a huge black eye to the sector and harmed students. Under this effort, high-performing sponsors would be rewarded, which would encourage authorizing best practices and improve the likelihood of greater quality control throughout all phases of a charter’s life cycle (start-up, renewal, closure).

While the conceptual framework for these sponsor-centric reforms is quite young, the reforms themselves are newer still. (House Bill 2 went into effect this February, and the previously enacted but only recently implemented sponsor evaluation is just now getting off the ground.) Even so, just five months in, HB 2 and the comprehensive sponsor evaluation system are already having an impact. Eleven schools were not renewed by their sponsors, presumably for poor performance, and twenty more are slated to close. Not only are academically low-performing schools prohibited under law from hopping to a new sponsor,ⁱ but it also appears that Ohio’s sponsors are behaving more cautiously in general—making it less likely that they will take on even mediocre performers (not just those for whom such prohibitions apply). Even more important, if the data in Graph 1 is any indication, sponsors seem to be applying caution to new school applicants as well—meaning that it’s far less likely that half-baked schools will open in the first place. Given Ohio’s recent track record of mid-year charter closures, this is a major victory, though a dramatically slowed opening rate sustained over time may indicate looming issues for the sector.

For the 2016–17 school year, the Ohio Department of Education lists just ten “potential” new charter schools, an all-time low in the number of charters opened in a given year. At least one is a replication of an existing top-notch school (Breakthrough’s Village Preparatory model). As Graph 1 depicts, this is significantly fewer compared to past years.

Graph 1: Charters opened each year, 1999–2016

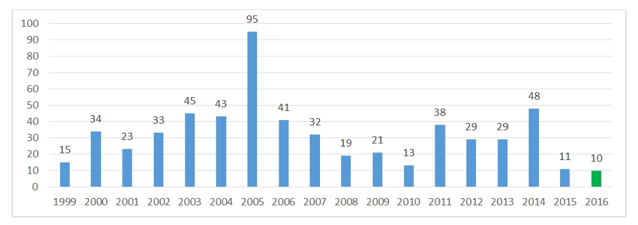
Source: Data come from the enrollment history listed in the Ohio Department of Education’s annual community schools report (2015).ⁱⁱ

In the days leading up to HB 2’s passage last October, we urged Ohio to expect more from charter school sponsors during the new school application process. “Closing poor performers when they have no legs left to stand on is only a small part of effective oversight. A far better alternative would be to prevent them from opening in the first place,” we wrote. “If Ohio charter schools are going to improve, better decision making about new school applicants will be critical.”

Ohio’s charter reforms appear to have influenced sponsor behavior in opening new schools. There are likely other reasons contributing to the overall slowdown—saturation in the academically challenged communities to which start-ups are restricted, for example, and a lack of start-up capital—but new, higher sponsor expectations and a rigorous sponsor evaluation system have undoubtedly played a sizeable role.

Sponsors await the first round of performance ratings this fall, with one-third of their overall scores tied to the performance of the schools in their portfolios. Fordham remains concerned that the academic component leans too heavily on performance indicators strongly correlated to demographics rather than student growth, making it difficult if not impossible for even good sponsors to earn high marks in this category. At a minimum, however, the rigor of the evaluation is spurring long-overdue changes to the new school vetting process and making all sponsors think long and hard before handing out charter contracts.

For the moment, slowing new charter growth in Ohio is a good thing. The state has just started down the path of serious charter school reform, and the sector, which was too lax for too long, is in need of balance. Like any pendulum, however, it’s possible that Ohio will move itself too far in the other direction—if the opening rate continues to stall, for instance, or even stops entirely. If even the state’s best sponsors can’t open new schools, the sponsor accountability framework will need revision so that families and students are not deprived of high-quality choices. Stagnant growth could also occur if Ohio charters continue to be starved of vital start-up funds. It is telling—and worrisome—that just one of Ohio’s proposed new charter schools is a replication of an existing high-quality network. It’s also troublesome that Ohio’s $71 million in federal Charter School Program funds—a program responsible for helping the state’s best charter networks start and expand—remains on hold.

Now that the state has accomplished the tough task of revising its charter law, Ohio needs to consider ways to make it easier for the best charters to expand and serve more students. Leaders of Ohio’s best charter schools point to inequitable funding, lack of facilities, and human capital challenges as serious impediments to growth. Lawmakers should explore ways to fast-track the replication of Ohio’s best charters while keeping an eye more broadly on preserving the autonomy of the sector, rewarding innovation and risk-taking, and resisting efforts to over-regulate. If we are serious about lifting outcomes for Ohio’s underserved children and preventing the sector from too closely mimicking traditional public schools, these issues demand our attention. For the time being, it’s worth celebrating early milestones indicating that Ohio is on its way to serious improvement.

[i] Low-performing charter schools—those receiving a D or F grade for performance index and a D or F grade for value-added progress on the most recent report card—cannot change sponsors unless several stipulations apply: the school finds a new sponsor rated effective or better, hasn’t switched sponsors in the past, and gains approval from the Ohio Department of Education.

[ii] The number of opens for 2014 slightly contradicts the number provided in my past article, “Expecting more of our gatekeepers of charter school quality.” This article lists forty-eight opens, per Ohio’s enrollment records. However, those same records list no students for several of the fly-by-night schools that did in fact open (and shut mid-year). The previous article counted those five schools for the purposes of illustrating the especially high numbers of poorly vetted schools opening in 2014.

• The mental image most people have of career and technical education is taken directly from a mid-century General Motors training video: Enthusiastic young men in denim replacing serpentine belts and laboring over alternators. Failing that, the scenario might take place in a wood shop or a welding station. But trainees at Willy’s Café—a student-run coffee shop in a Willamette, Oregon, high school profiled this week on NPR—are picking up a different set of professional skills. The program is one of an assortment directed by the Distributive Education Clubs of America (DECA), a venerable vocational initiative that specializes in retail and marketing training, and its student-workers are there to absorb the basics of professional comportment. As part-time baristas, bank tellers, and graphic designers, they’re acquiring the “soft skills” of customer service that will make them valuable to future employers, especially if they choose to supplement them with a college degree or two-year certificate. Even better, they don’t have to deal with engine grease on their overalls.
• The fight over Common Core was basically a local foofaraw blown into a national story by political opportunists. In case you’re just coming back from a half-decade mission to Saturn: The standards were adopted by state legislatures as a means of improving instruction, but they expressly left it to district- and school-level practitioners to decide how to reach the more rigorous benchmarks. Now we’re starting to see stories like this one, from Ohio’s out-of-the-way Mercer County, where superintendents and principals are approvingly reporting that the United Nations’ black helicopters have stayed grounded and local control has been preserved. Now that Common Core is pretty much here to stay, there’s something amusing in hearing folks finally discover for themselves the good news that its advocates have been trying to spread since President Obama’s first term (“Nope, turns out it’s actually not a curriculum. Or an education takeover masterminded by the One World Government, actually”). On second thought, nah—none of this is funny at all. I’ll take the last few years of my life back, please. 
• For such a carefree band of swashbuckling choice advocates, we at Fordham have always been fairly tough on online charter schools. That’s because a whole lot of virtual charters—and we’re not alone in this discovery—kinda suck. Our own report on Ohio’s troubled crop of e-schools is due out next month, but most observers agree that the sector is plagued by chronic academic underperformance that leaves its students years behind their traditional public school counterparts. We shouldn’t close the door to online schools’ potential just yet, though; online instruction is an approach with natural appeal for thousands of students with irregular home lives, health complications, or highly mobile families. In Education Next, Tom Vander Ark and Greg Richmond give a good summation of the lousy status quo and a few suggestions on how to improve matters. In a world where virtual charters obviously aren’t going anywhere for the time being, we could do worse than heed their suggestions.

On this week’s podcast, Mike Petrilli, Robert Pondiscio, and Brandon Wright discuss times tables, virtual charter school struggles, and charter school discipline. During the Research Minute, Amber Northern explains what we can learn from charter lotteries.

Amber's Research Minute

Julia Chabrier, Sarah Cohodes, and Philip Oreopoulos, "What Can We Learn from Charter School Lotteries?," NBER (July 2016).

Spend any time at all writing education commentary and you’ll inevitably find yourself coming back to certain ideas and themes. Here’s one that I can’t stop probing and poking at like a sore tooth: Why do we insist on making teaching too hard for ordinary people to do well? It seems obvious that we’ll never make a serious dent in raising outcomes for kids at scale until or unless we make the job doable by mere mortals—because that’s who fills our classrooms. So go nuts: Beat the bushes for 3.7 million saints and superheroes. Raise standards. Invest billions in professional development (with nearly nothing to show for it). Or just give teachers better tools, focus their efforts, and ask them to be really good at fewer things.

The latest data point to illustrate this idea—that maybe we should make teaching an achievable job for average people—comes from C. Kirabo Jackson and Alexey Makarin, a pair of researchers at Northwestern University. Their intriguing new study suggests that teacher efficacy can be enhanced—affordably, easily, and at scale—by giving teachers “off-the-shelf’ lessons designed to develop students’ deep understanding of math concepts.

The pair randomly assigned teachers in three Virginia school districts to one of three groups. The first was given free access to online lessons “designed to develop understanding.” (the Mathalicious curriculum, an “inquiry-based math curriculum for grades six through twelve grounded in real-world topics”). To promote adoption of these lessons, a second group of teachers was assigned to the “full treatment” condition, which included free access to the lessons, email reminders to use them, and an online social media group focused on implementing them. A third group of teachers went about business as usual. If the best teachers are those who can simultaneously impart knowledge and develop students’ understanding, Jackson and Makarin wanted to see if teachers “who may only excel at imparting knowledge” might be more effective overall if given lessons to teach that were aimed at deep understanding of math concepts.

The unsurprising upshot is that it worked. “Full treatment teachers increased average student test scores by about 0.08 standard deviations relative to those in the control group. Benefits were much larger for weaker teachers, suggesting that weaker teachers compensated for skill deficiencies by substituting the lessons for their own efforts,” the pair note. In other words, access to good lessons simplified the complex job of teaching and allowed for greater specialization—fewer moving parts, more focused effort, better results.

It is easy to look at the modest effect size of the intervention, a mere 0.08 standard deviations, and ask (cue Peggy Lee), “Is that all there is?” But as Jackson and Makarin note, while the results seem modest, “this is a similarly sized effect as that of moving from an average teacher to one at the eightieth percentile of quality, or reducing class size by 15 percent.” And much, much cheaper. The estimated cost of the intervention was about $431 per teacher, and each teacher has about ninety students on average. “Back-of-the envelope calculations suggest that the test score effect of about 0.08? would generate about $360,000 in present value of student future earnings.” In sum, this “modest” return on a vanishingly small investment offers “an internal rate of return far greater than that of well-known educational interventions such as the Perry Pre-School Program, Head Start, class size reduction, or increases in per-pupil school spending.”

Not surprisingly—and most persuasively—the effects of giving teachers good lessons were “much larger for weaker teachers, suggesting that weaker teachers compensated for skill deficiencies by substituting the lessons for their own efforts.” Give a weak teacher good lessons to teach—allow them to focus on lesson delivery, not lesson design—and they get better results. Who’d have thunk?

Are these results replicable? Does it work across subject disciplines? Would better curricula show even larger effects? There is more work to be done, but the principle is now firmly established: Curriculum effects are real, significant and cheap.

Now tell me again: Why curriculum isn’t at the top of our priority list of reform levers when it offers much bigger bang for far fewer bucks? And why we aren’t using it to make teachers’ lives easier and their jobs more doable?

SOURCE: C. Kirabo Jackson and Alexey Makarin, “Simplifying Teaching: A Field Experiment with Online “Off-the-Shelf” Lessons,” National Bureau of Economic Research (July 2016).

A new experimental study examines whether interim assessments have an effect on improving outcomes for students at the lower, middle, and higher ends of the achievement distribution, with a particular focus on the lower end.

Specifically, researchers study two reading and math assessment programs in Indiana: mCLASS in grades K–2 (a face-to-face diagnostic for which teachers enter results immediately in a hand-held device) and Acuity, a CTB/McGraw Hill product, in grades 3–8 (which is administered via paper/pencil). K–8 schools that volunteered to take part in the study and met certain criteria (like not having used the two interim assessments before) were randomly assigned to treatment and control conditions in the 2009–10 academic year. Of the 116 schools that met all criteria, seventy were randomly selected to participate, fifty-seven were assigned, and fifty ultimately participated. The outcome measure for grades K–2 was the Terra Nova; for grades 3–8, the Indiana state test (ISTEP+). The analysts conducted various analyses, each of which targeted impact at the lower, middle, and upper tail of the distribution.

In general, the results show that in grades 3–8, lower-achievers seem to benefit more from interim assessments than higher-achieving students. The magnitude of the effects were larger in math than reading; in some cases the estimates for math were larger than one-fifth of a standard deviation, which is sizable. However, the treatment on treatment results (i.e., the fifty schools that participated) show that reading and math results were both insignificant at grade K–2, which used mCLASS.

Analysts posit various reasons for the lack of results at K–2: mCLASS is not as effective as Acuity; effects of tests like these aren’t as visible in the early grades; and the mCLASS impact was not adequately captured by the Terra Nova assessment, nor is mCLASS aligned to Terra Nova, nor is TerraNova aligned to Indiana standards! On the other hand, ISETEP is used for accountability purposes, so teachers are more likely to pay attention to interim assessment results.

Bottom line: At least in this study, interim assessments don’t have much effect on improving outcomes for average or high-performing students—just the low-performers. So about those parents of high-achievers who complain about too much testing for their kids…well, they may have a point.

SOURCE: Spyros Konstantopoulos, Wei Li, Shazia R. Miller, and Arie van der Ploeg, "Effects of Interim Assessments Across the Achievement Distribution: Evidence From an Experiment," Educational and Psychological Measurement (June 2016).